수학 영역은 2007 개정 수학과 교육과정의 내용과 수준에 근거하고, 대학 교육에 필요한 수학적 사고력을 측정하는 문항을 출제하고자 하였다. 구체적인 출제 원칙은 다음과 같다.
◦ 평가 목표는 2007 개정 수학과 교육과정의 목표와 내용에 기초하여 설정하였다.
◦ 교육과정의 내용을 충실히 반영하여 고등학교 수학교육에 긍정적인 영향을 미칠 수 있는 문항을 출제하고자 하였다.
◦ 고등학교까지 학습을 통해 습득한 수학의 개념과 원리를 적용하여 문제를 이해하고 해결하는 능력을 측정할 수 있는 문항을 출제하는 데 중점을 두었다.
◦ 복잡한 계산을 해야 하는 문항의 출제를 지양하고, 반복 훈련으로 얻을 수 있는 기술적 요소나 공식을 단순하게 적용하여 해결할 수 있는 문항보다는 교육과정에서 다루는 기본 개념에 대한 충실한 이해와 종합적 사고력을 필요로 하는 문항을 출제하고자 하였다.
수학 A형과 수학 B형은 교육과정의 내용과 수준을 고려하여 출제하였다. 수학 A형은 ‘수학Ⅰ’, ‘미적분과 통계 기본’ 내용 전체에서 출제하였고, 수학 B형은 ‘수학Ⅰ’,‘수학Ⅱ’, ‘적분과 통계’, ‘기하와 벡터’ 내용 전체에서 출제하였다.
수학 영역은 고등학교 수학과 교육과정에 제시된 수학의 기본 개념, 원리, 법칙을 이해하고 적용하는 능력을 평가하는 문항, 수학에서 중요하게 다루어지는 기본 계산 원리 및 전형적인 문제 풀이 절차인 알고리즘을 이해하고 적용하는 능력을 평가 하는 문항, 규칙과 패턴, 원리를 발견하고 논리적으로 추론하는 문항, 주어진 명제의 참, 거짓을 판별하는 능력을 평가하는 문항, 주어진 풀이 과정을 이해하고 빈 곳에 알맞은 식 또는 값을 찾을 수 있는 능력을 평가하는 문항을 출제하였다. 또한 두 가지 이상의 수학 개념, 원리, 법칙을 종합적으로 적용하여야 해결할 수 있는 문항과 실생활 맥락에서 수학의 개념, 원리, 법칙 등을 적용하여 해결하는 문항도
출제하였다.
수학 A형과 수학 B형의 출제 범위 및 수준 차를 고려하여 각 30문항 중에서 4문항을 공통으로 출제하였다. 구체적으로, 디지털 사진을 압축할 때 원본 사진과 압축한 사진의 다른 정도를 나타내는 지표가 포함된 식을 이용하여 주어진 문제를 해결하는 문항(A형 10번, B형 25번), 행렬의 성질을 이해하고 두 이차정사각행렬에
대한 식의 참, 거짓을 판별하는 문항(A형 19번, B형 16번), 주어진 등비수열을 이용하여 무한등비급수의 합을 구하는 문항(A형 11번, B형 7번), 행렬의 연산에 관한 문항(A형 2번, B형 1번)을 출제하였다.
수학 A형에서는 등비수열의 뜻을 알고 있는지를 묻는 문항, 다항함수의 정적분을 구할 수 있는지를 묻는 문항, 이항정리를 이해하고 있는지를 묻는 문항, 함수의 연속에 대한 개념을 이해하고 좌극한, 우극한을 구할 수 있는지를 묻는 문항, 수열의 일반항과 합과의 관계를 이해하고 있는지를 묻는 문항, 정규분포의 뜻과 성질을 이해하고 있는지를 묻는 문항, 다항함수의 미분의 개념을 이해하고 이를 활용할 수 있는지를 묻는 문항, 지수부등식의 해를 구할 수 있는지를 묻는 문항, 조건부 확률의 뜻을 알고 이를 구할 수 있는지를 묻는 문항, 중복조합의 수를 구할 수 있는지를 묻는 문항, 함수의 그래프 개형을 이해하고 미분을 이용하여 문제를 해결할
수 있는지를 묻는 문항, 로그함수의 그래프를 활용하여 문제를 해결할 수 있는지를 묻는 문항 등을 출제하였다.
수학 B형에서는 삼각함수의 합성을 이용하여 삼각함수의 최댓값을 구할 수 있는지를 묻는 문항, 좌표공간에서 선분의 내분점의 좌표를 구할 수 있는지를 묻는 문항, 일차변환의 성질을 이해하고 이를 활용할 수 있는지를 묻는 문항, 확률의 덧셈정리를 이해하고 이를 활용할 수 있는지를 묻는 문항, 포물선의 뜻을 이해하고 이를 활용할 수 있는지를 묻는 문항, 삼수선의 정리를 이해하고 있는지를 묻는 문항, 조건부 확률을 이해하고 이를 이용하여 확률을 구할 수 있는지를 묻는 문항, 수열의 일반항을 추론하는 과정을 이해할 수 있는지를 묻는 문항, 좌표공간에서 직선의 방정식을 이해하고 내적의 성질을 활용할 수 있는지를 묻는 문항, 무리방정식의 해를 구할 수 있는지를 묻는 문항, 타원의 뜻을 이해하고 그 성질을 활용할 수 있는지를 묻는 문항, 미분의 정의를 이해하고 이를 활용하여 문제를 해결할 수 있는지를 묻는 문항 등을 출제하였다.
수학 영역은 A형과 B형 모두 적정 난이도를 유지하고 일정 수준의 변별력을 확보하고자 노력하였다. 이를 위해 기본적인 수학적 사고력을 측정하기 위한 쉬운 문항들과 중간 수준 난이도의 문항들을 중심으로 시험을 구성하되, 상위권 변별을 위해 고차적인 사고력을 요구하는 문항들도 출제하였다. 또한 수학과 교육과정의
내용과 수준에 맞춰 A형과 B형 시험의 난이도를 차별화하고자 하였다.
◦ 수학 영역에서는 출제 범위에 속하는 과목의 내용과 수준에 근거하여, 고등학교 교육과정을 정상적으로 이수한 수험생에게 적합한 문항을 출제하였다.
◦ 교육과정상의 중요도, 내용 수준, 소요 시간, 난이도 등을 고려하여 2점, 3점, 4점으로 차등 배점하였다. 수학 A형과 수학 B형 모두 전체 문항 수의 30%를 단답형 문항으로 출제하였고, 답은 세 자리 이하 자연수가 나오도록 하였다.
◦ 수학 A형은 ‘수학Ⅰ’ 15문항, ‘미적분과 통계 기본’ 15문항으로 구성하였다. 수학 B형은 ‘수학Ⅰ’ 8문항, ‘수학Ⅱ’ 7문항, ‘적분과 통계’ 8문항, ‘기하와 벡터’ 7문항으로 구성하였다. 또한 ‘수학Ⅰ’의 4문항을 공통으로 출제하여 2014학년도 수능에서의 공통 문항의 수를 유지하였고, 공통 문항의 문항 번호는 달리하였다.
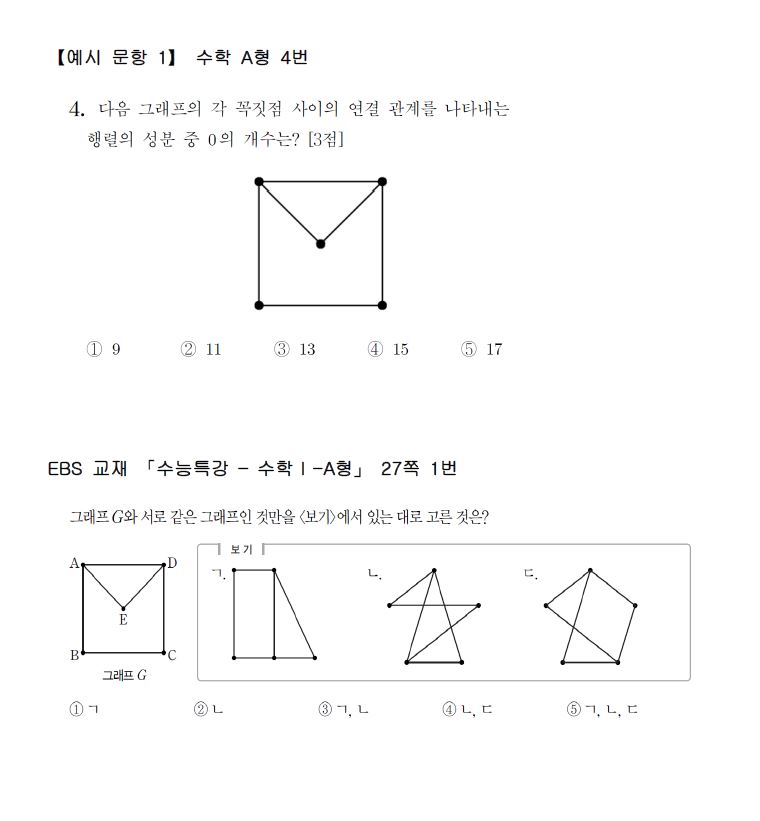
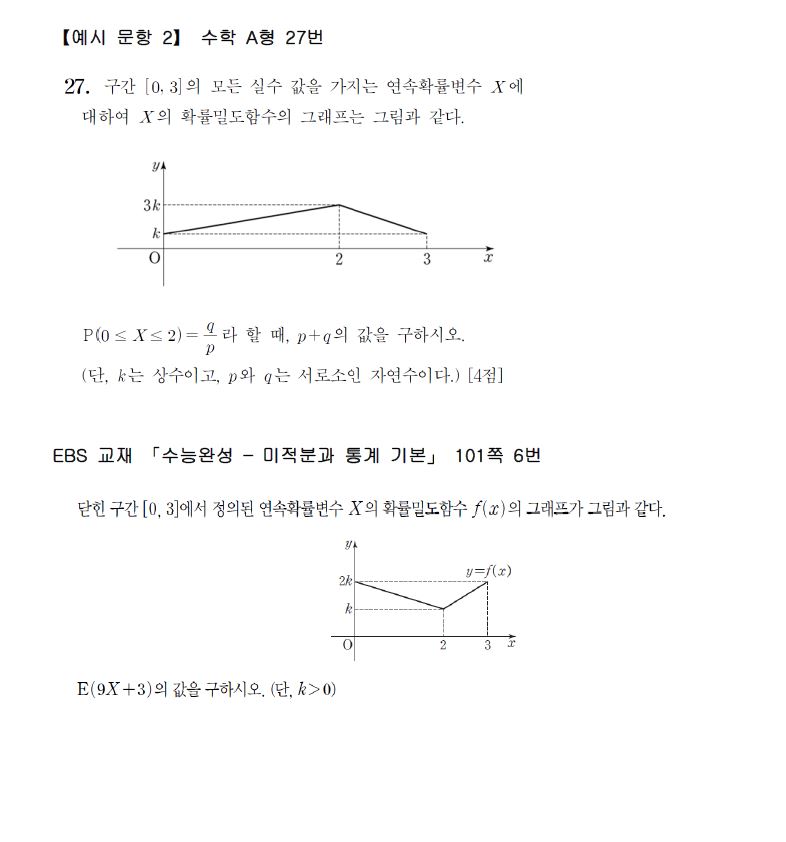
수학 영역에서 연계하여 출제된 문항을 EBS 교재 문항과 비교하여 제시하면 다음과 같다.
전자신문인터넷 라이프팀
신지혜기자 sjh123@etnews.com







